Union-Find Algorithm

2021-06-13-Algo-REVIEW

Graph Algo?

• graph 란 Node와 Node사이에 연결된 Edge 의 정보를 가지고 있는 자료구조

	Graph	Tree
방향성	방향 그래프 혹은 무방향	방향 그래프
순환성	순환 혹은 비순환	비순환
루트 노드 존재 여부	루트 노드 없읍	루트 노드 존재
노드간 관계성	부모와 자식 관계가 없음	부모와 자식 관계
모델의 종류	네크워크 모델	계층 모델

• 그래프 구현 방법은 2가지가 존재한다. (메모리와 속도 측면에서 다른 결과를 보임)
  • 인접행렬 : 2차원 배열을 사용하는 방식
  • 인접 리스트 : 리스트를 사용하는 방식

	Memory space	Time
인접 행렬	O(V2)	O(1)
인접 리스트	O(E)	O(V)

서로소 집합 (Disjoints Sets)

• 공통 원소가 없는 두 집합을 의미하는 자료구조
  위 자료구조를 처리하기 위해서는 Union, Find 2개의 연산으로 처리해야한다.

1. Union

• 두 원소가 속한 집합을 합치는 함수

 private static void union(int a, int b){
        a=find(a);
        b=find(b);
        if(a<b) parent[b]=a;
        else parent[a]=b;
    }

2. Find

• x가 속한 집합의 대표값(루트 노드 값)을 반환한다. 즉, x가 어떤 집합에 속해 있는지 찾는 연산

[비대칭 트리구조]
private static int find(int x){
        if(x==parent[x]) return x; // 자기 자신의 루트 노드 라는 의미
        return find(parent[x]);
    }

비대칭 트리구조 형태일 경우 연결 리스트 형태로 구성되어 배열로 구현하는 방식보다 시간 복잡도가 O(N) 이 되어 비효율적인 구성이 된다.

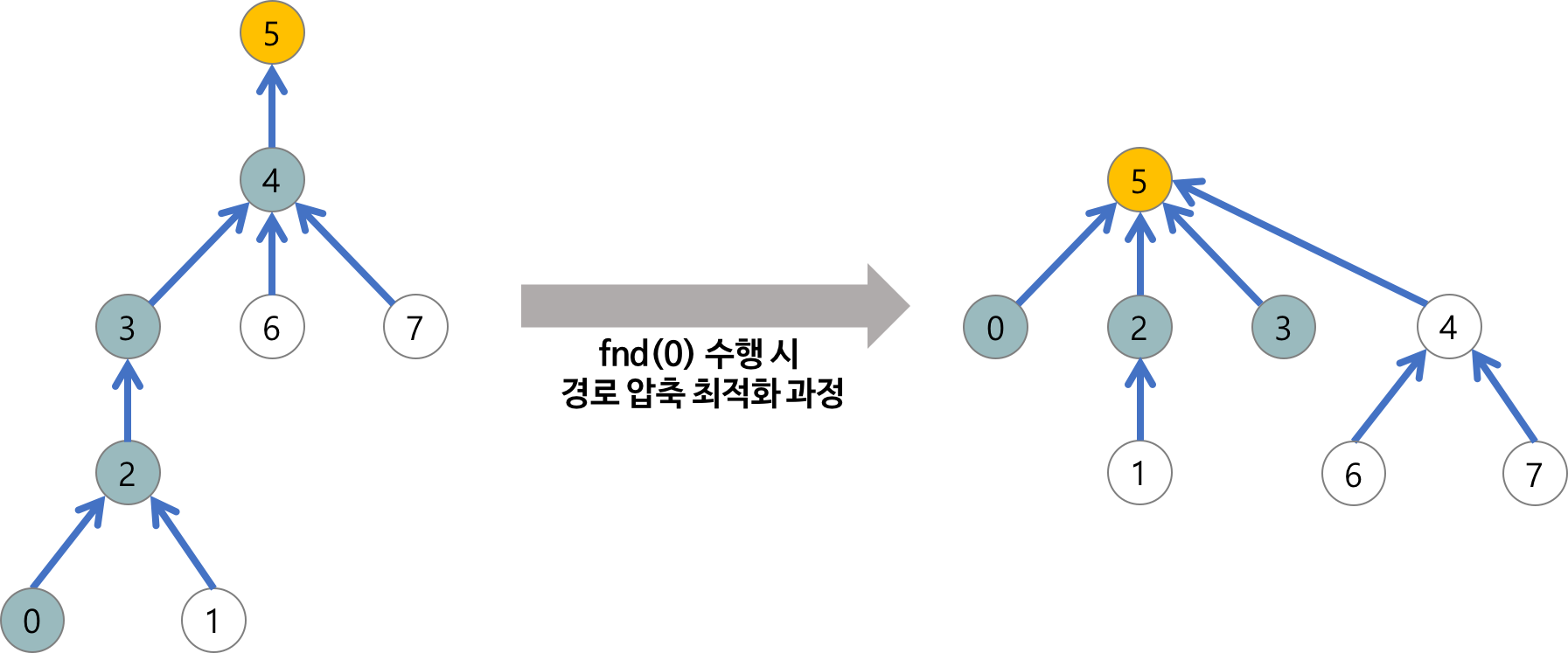
시간 복잡도를 개선하기위해서는 리스트 형태의 트리 구조를 경로압축 과정을 통해 시간복잡도가 O(lonN) 인 균형있는 트리 구조로 개선해야한다.

\[대칭 트리구조\]  
private static int find(int x){  
if(x==parent\[x\]) return x; // 자기 자신의 루트 노드 라는 의미  
return parent\[x\]=find(parent\[x\]);  
}

---

• 두 함수를 같이 구성하여 Union-find 알고리즘 과정을 표현할 수 있다. 이 과정으로 통해 크루스칼 알고리즘 을 표현할 수 있게 된다.
  

---

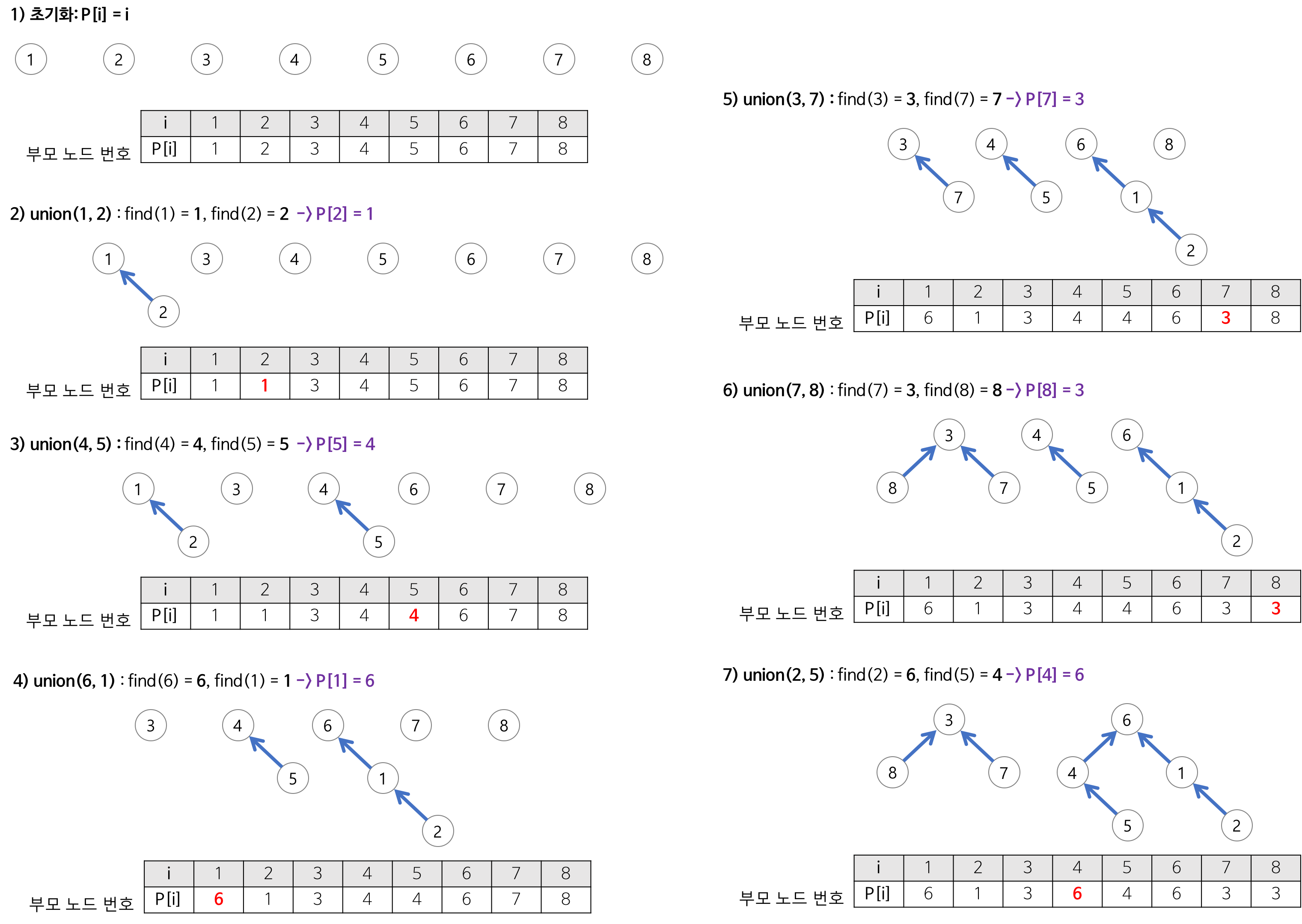
Union-Find 알고리즘의 무한 순회

• Union-Find 알고리즘을 구현할 경우 Find 함수에서 무한 순회가 발생할 경우 Union 함수를 수행할 수 없게 된다.
  Cycle 판단하는 함수를 구성하여 자기자신의 노드를 마주했을 때 함수를 빠져 나가 Union 함수를 수행하도록 해야한다.

  boolean cycle = false;

  for(int i=1; i<=e; i++){
  int a= sc.nextInt();
  int b = sc.nextInt();
  if(find(a)==find(b)){
   cycle = true;
   break;
   }
   else
  union(a,b);
  }

최소한의 비용으로 모든 노드를 순회(Kruskal Algorithm)

크루스칼 알고리즘은 신장트리 자료구조를 기반으로 하며 작은 비용으로 모든 노트를 순회를 목적으로 한다.
이때 시간 복잡도는 O(ElogE) 이다.

( 신장트리 : 하나의 크래프가 존재할 때 모든 노드를 포함하면서 사이클이 존재하지 않는 그래프)

1. 간선의 크기에 따라 오름차순 정렬
2. 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생하는지 판단(Union-Find Algorithm)
3. 모든 간선에 대해 2번의 과정을 반복

---

🙆‍♂ 예시 코드 링크

• [Union-Find Algorithm]( )
• [Union-find Cycle Algorithm]( )
• [Kruskal Algorithm]( )

🧾 Reference

• 이것이 코딩 테스트다 whit Python
• Union-Find 알고리즘