티스토리 뷰
반응형
Longest Increasing Subsequence(LIS)
최장 증가 부분 수열(Longest Increasing Subsequence) 문제는, 주어진 수열에서 오름차순으로
정렬된 가장 긴 부분수열을 찾는 문제이다. 여기서의 부분 수열은 연속적이거나 유일할 필요는 없다.
최장 증가 부분 수열 문제는 입력 수열의 길이가 n일 때 O(N^2)의 시간에 풀이가 가능하다.
구현
1. 개념
증가 부분 수열을 만들기 위해서는 2중 loop 문(i, j)으로 순회하면서 하나의 i 이전까지 순열중에서 가장 긴 배열을 선택하면 된다.
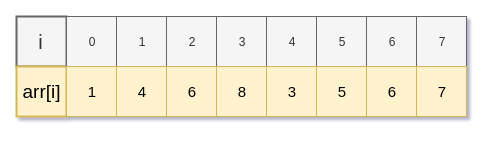
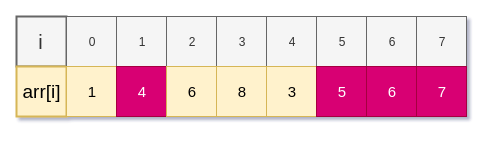
모든 index를 순회하면서 각 인덱스의 LIS는 다음과 같다.
최종적으로 위 배열에서 LIS 값은 4 이다.
| Index(i) | arr | Index(i) | arr |
|---|---|---|---|
| i=0 | {1} | i=4 | {1,4,6,8} |
| i=1 | {1,4} | i=5 | {1,4,6,8} |
| i=2 | {1,4,6} | i=6 | {1,4,6,8} |
| i=3 | {1,4,6,8} | i=7 | {4,5,6,7} |
2. 위 문제로 도출해 낼 수 있는 공식은?
- 정수 i, j에 대해 i < j이면, S[i] < S[j]다.(0 <= i, j <= |S|)
- 정수 i, j에 대해 S[i] < S[j]이면, 원 배열 arr에서의 S[i], S[j] 두 수의 위치 전후관계는 같다.(0 <= i, j <= |S|)
LIS 구현하는 2가지 방법(with. 가장 긴 증가하는 부분 수열)
1. 동적 계획법
주어진 arr 배열에서 조건에 적합한 dp 배열을 채워 나가는 방법으로 시간 복잡도는 O(N^2) 이다.
public class back_11053 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int arr[] = new int[n];
int d[] = new int[n];
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
Arrays.fill(d,1);
for(int i=1; i<n; i++){
for(int j=0; j<i; j++){
if(arr[j]<arr[i] && d[i] <= d[j])
d[i] = d[j]+1;
}
}
int max = 0;
for(int i: d){
max = Math.max(i,max);
}
System.out.println(max);
}
}2. 이진탐색
시간복잡도는 O(NlogN)
public class back_11053 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int arr[] = new int[n];
StringTokenizer st = new StringTokenizer(br.readLine()," ");
List<Integer> list = new ArrayList<>();
list.add(0);
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
for(int i = 0 ; i < n; i++) {
int value = arr[i];
if(value > list.get(list.size() - 1)) list.add(value);
else{
int left = 0;
int right = list.size() - 1;
while(left < right){
int mid = (left + right) >> 1;
if(list.get(mid) >= value){
right = mid;
}else{
left = mid + 1;
}
}
list.set(right, value);
}
}
System.out.println(list.size() - 1);
}
}🧾Reference
반응형
'알고리즘' 카테고리의 다른 글
| Back Tracking에 대해 알아보자 (0) | 2022.03.06 |
|---|---|
| 최대 부분 합 구하기 - Kadane's_Algorithm (0) | 2022.03.02 |
| 최소신장트리 알고리즘 (0) | 2022.02.26 |
| Leven Shtein Algorithm (0) | 2022.02.26 |
| Union-Find Algorithm (0) | 2022.02.26 |
반응형
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 면접
- 스프링
- C언어
- ajax
- nginx
- Algorithm
- CS
- 자격증
- Matlab
- java
- 자바
- kakao
- 알고리즘
- OOP
- 디자인패턴
- security
- 프로그래머스
- docker
- spring-cloud
- 매트랩
- Spring
- 릿코드
- 그래프
- 백준
- springboot
- Solid
- interview
- JPA
- 수학
- 스프링부트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
글 보관함
